استاندارد رمزنگاری پیشرفته (به انگلیسی: Advanced Encryption Standard) یا به اختصار AES مشخصهای برای رمزنگاری دادههای دیجیتال است که در سال ۲۰۰۱ توسط مؤسسه ملی فناوری و استانداردهای ایالات متحده ایجاد گردید.این رمز که در ابتدا ریندال(به انگلیسی: Rijndael) نامیده میشد و توسط دو رمزنگار بلژیکی به نامهای ژوآن دیمن (به انگلیسی: Joan Daemen) و وینسنت رینمن (به انگلیسی: Vincent Rijmen) توسعه داده شد
استاندارد رمزنگاری پیشرفته توسط دولت ایالات متحده پذیرفته شده و اکنون در سراسر جهان استفاده میگردد. این الگوریتم رمزنگاری به جای استاندارد رمزنگاری دادهها (DES) که در سال ۱۹۷۷ منتشر شده،جایگزین گردیدهاست. الگوریتم AES یک الگوریتم کلید متقارن است، بدین معنی که از یک کلید یکسان برای رمزنگاری و رمزگشایی استفاده میشود
سلام
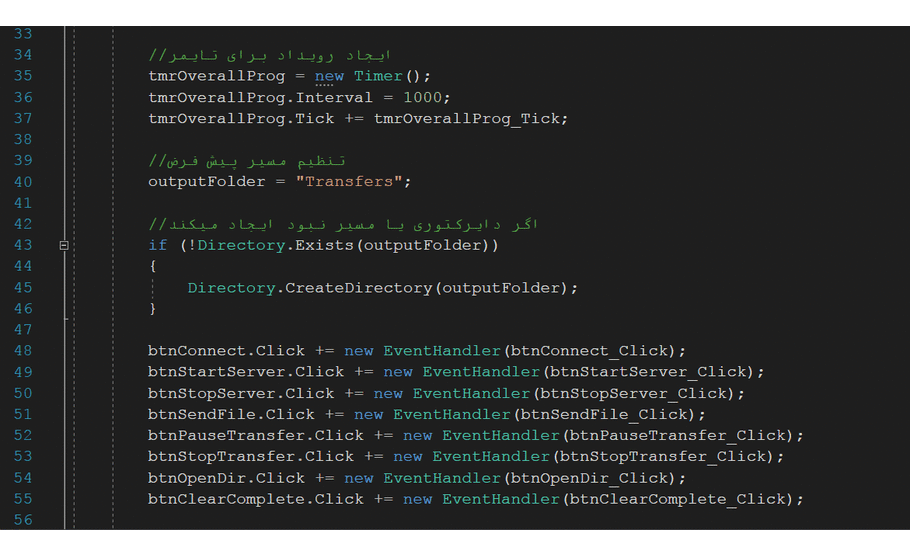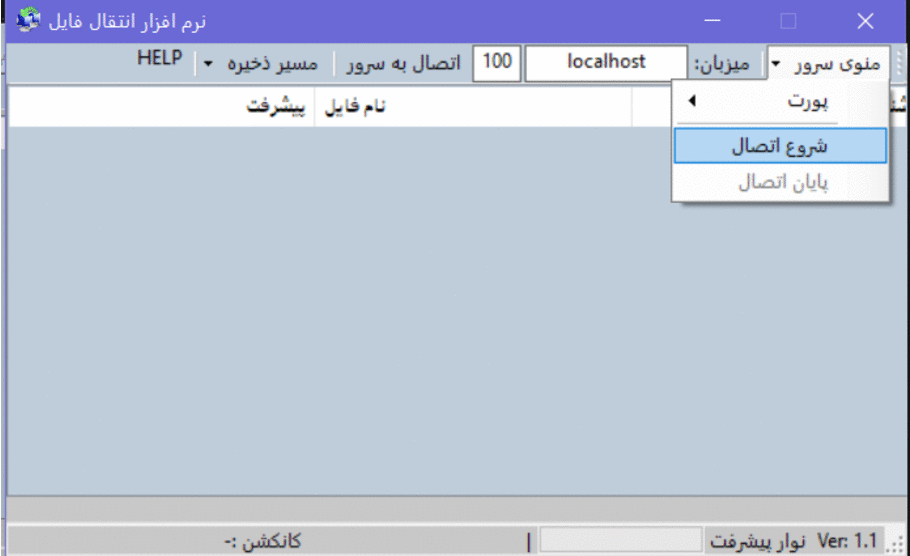
یه برنامه از سوکت براتون قرار میدم تقریبا 20 روزه کار کردم تقریبا روی یک فرم کار کردم ایراداتی که داشته رو برطرف کردم البته سوکت نویسی کار ساده ای نیست کار با پروتکل های سوکت و بکارگیری انها در جا خود بسیار سخته البته اونایی که میگن سی شارپ سادس لابد یا خیلی باهوشن یعنی بالای140 من که باهوش نیستم اما کندذهنم نیستم ولی میدونم یادگیری سی شارپ به این راحتی ها نیست درصد پیچیدگی سی شارپ بعد ا جاوا اسکریپت و سی در سطح سومه البته نشد نیست و نداره اینها توسط افرادی مثل منو شما تدوین و برنامه نویسی شدن
سفارش و طراحی وب سایت
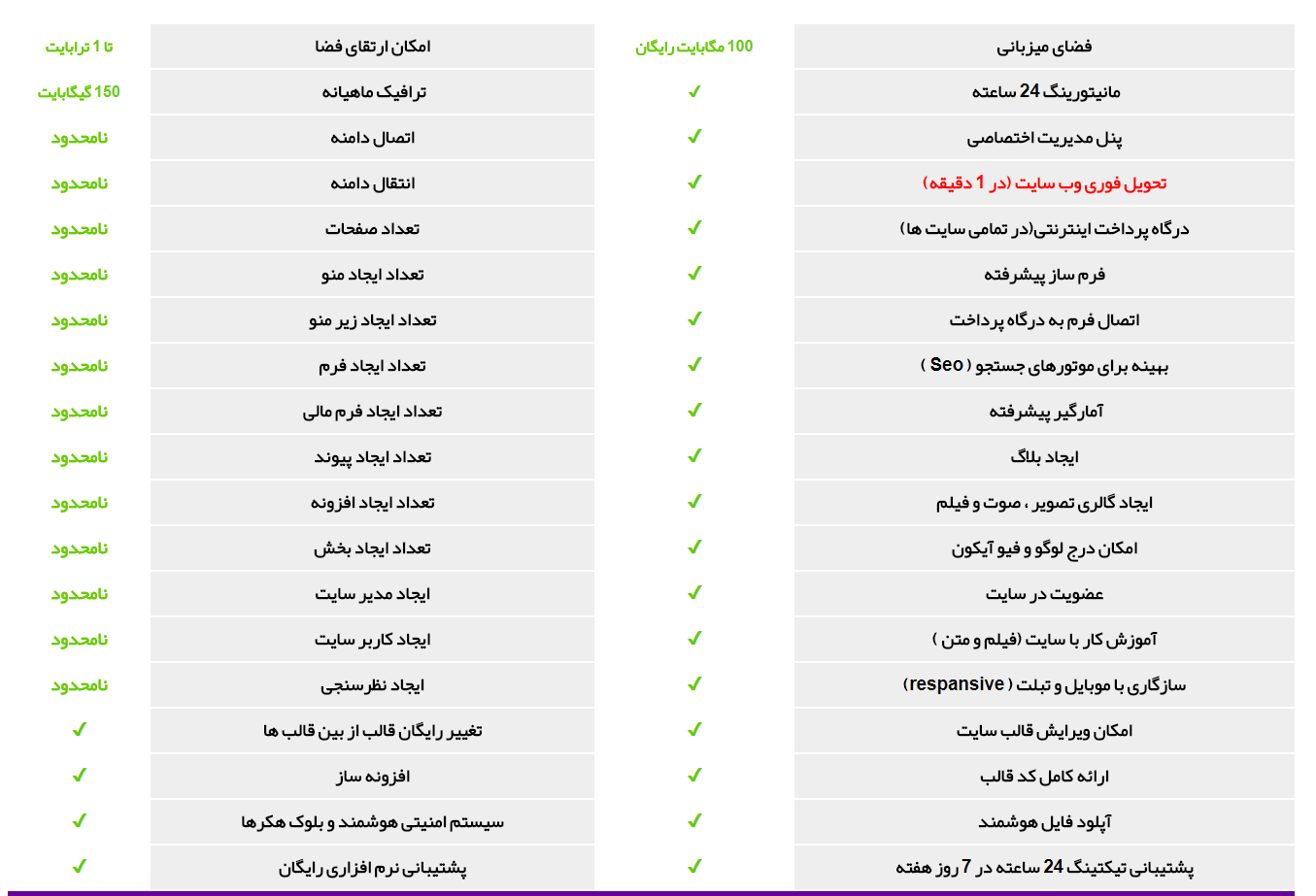
با این قیمت نمیتونید چنین سایتی تهیه کنید
قیمت هاست و سایت 285 هزار تومان با امکانات بالا میتونید امکانات رو در ادامه مطلب مشاهده کنید
ا توجه به نوپا بودن فروشگاه های اینترنتی در ایران و کمبود فروشگاه های اینترنتی تخصصی در کشور ، اگر همین امروز اقدام به فعال سازی فروشگاه اینترنتی خود نمایید قطعا رقبای زیادی را پشت سر می گذارید. یک فروشگاه خوب و پر بازدید علاوه بر داشتن کالاهای با کیفیت ، اصل و ارائه خدمات گارانتی و ضمانت هایی نظیر بازگشت کالا و تحویل سریع و غیره نیاز به برنامه نویسی قدرتمند ، سرعت بالا در لود شدن و همچنین طراحی زیبا و قابل دسترس برای مشتریان دارد. فروشگاه ساز یوتاب تمامی مزایای فوق را برای شما در لحظه فراهم می کند . همین حالا سایت خود را سفارش دهید و در همین لحظه فروشگاه قدرتمند و حرفه ای خود را دریافت نمایید.
سازمان های بزرگ به دلیل نوع خدمات دهی خود همیشه با حجم زیادی از مراجعه کنندگان مواجه هستند و انبوه جمعیت معمولا خستگی و کلافگی برای کارمندان و نارضایتی برای ارباب رجوع را به همراه دارد. بسیاری از کارها نظیر ثبت نام ، پرسیدن سوالات و بسیاری از کارهای کوچک بنابر حوزه فعالیت هر سازمان ، مسبب این شلوغی و نارضایتی می باشد. با داشتن یک سایت در زمان و هزینه هایی همچون مکان ، پرسنل ، تبلیغات و ... صرفه جویی می شود و برای ارائه اطلاعات به مشتریان دیگر نیازی به صرف هزینه نیست . وبسایت شما نماینده 24 ساعته ایست که به مراجعینتان اطلاعات دقیق و جامعی را می دهد. سایت های سازمانی یوتاب وب جایگاهی امن برای تمام کسانی است که به اهمیت دنیای مجازی پی برده و خواهان حضور در آن هستند
نام این الگوریتم بر اساس نام ارائهدهنده هلندی آن، یعنی اِدسخِر دایکسترا انتخاب شدهاست. در منابع فارسی آن را به شکلهای دِیکسترا، دکسترا، دایکسترا، دایجسترا، دیجسترا، دایجکسترا و دیجکسترا هم نوشته شده است، ولی جیمِ آن در تلفظ هلندی آن تلفظ نمیشود، لذا دو مورد اول صحیح هستند.
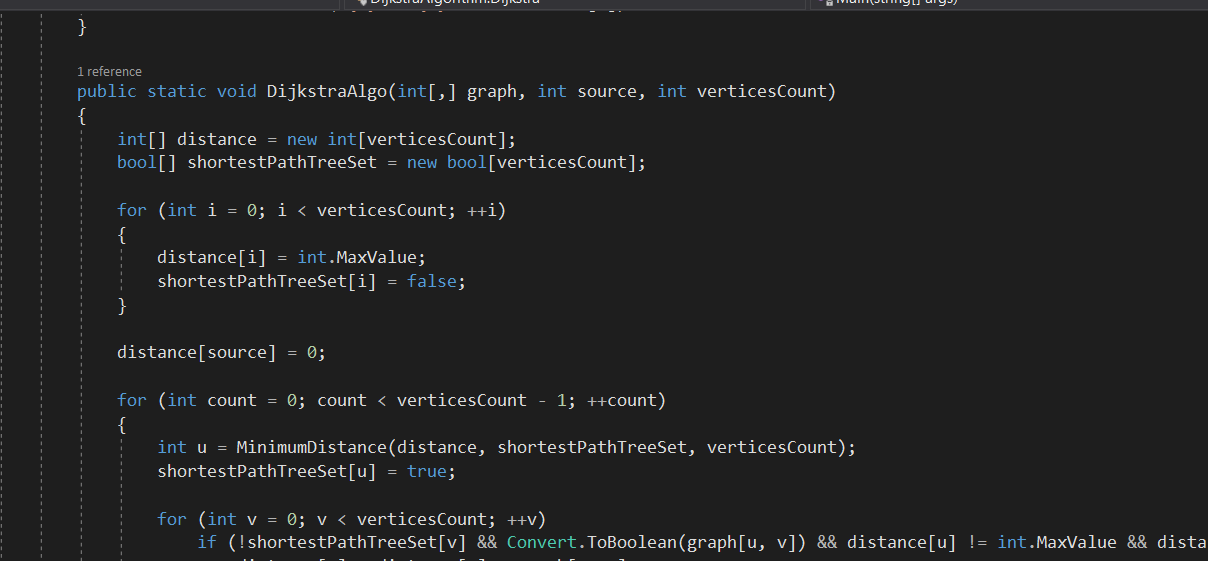
الگوریتم دایجسترا راهکاری برای پیدا کردن کموزن مسیر از رأس مشخص آغاز به بقیه رئوس در گراف جهتدار و وزندار (با وزنهای مثبت) میدهد. وزن یک مسیر در گراف وزندار برابر مجموع وزن یالهای آن است. جهتدار نبودن یالها هم مشکلی ایجاد نمیکند و میتوان برای یالهای غیر جهتدار دو یال فرض کرد.
لگوریتم
فرض کنید 1≤s≤n که در آن رأس s رأس آغاز است و فرض کنید:
dist(r)=0
و به ازای هر v≠r:
dist(v)=∞
فرض کنید مجموعهی T برابر رئوسی باشد که تا کنون کم وزنترین مسیر آنها را پیدا کردهایم. این الگوریتم در هر مرحله نزدیکترین رأس به s را که تا کنون به مجموعهی T اضافه نشده را انتخاب میکند (مثلا x) و آن را به مجموعهی T اضافه میکند و فاصلهی دیگر رأسها را با توجه به فاصلهی x بروز میکند. به ازای هر رأس v خارج T:....
سی شارپ دارای یک سامانه نوع یکپارچهاست که به آن CTS میگویند. این بدان معناست که تمام انواع، شامل موارد اصلی مانند Integerها، مشتق شده از System.Object هستند. به عنوان مثال، هر نوع یک متد به نام ToString() را به ارث میبرد. بخاطر کارایی، انواع اولیه (و انواع مقداری) بهطور داخلی فضایی برای آنها بر روی پشته در نظر گرفته میشود
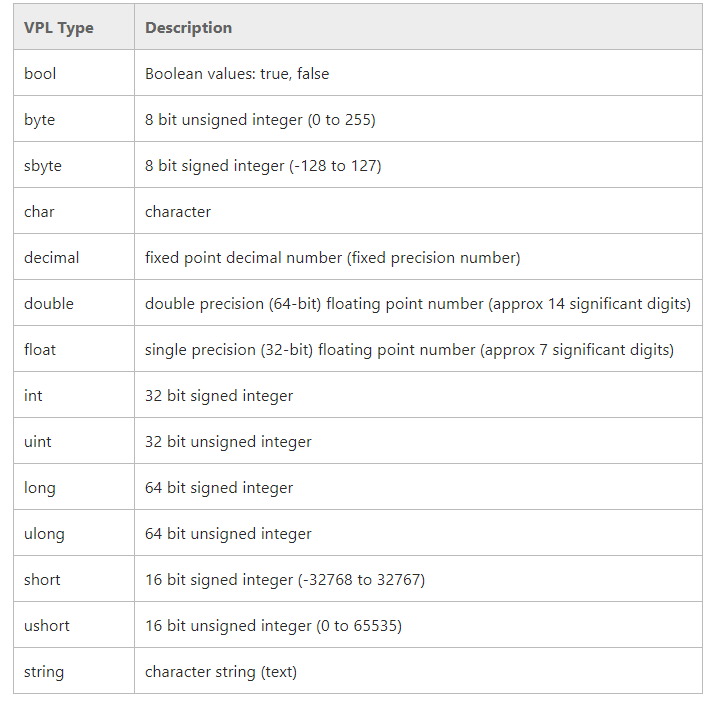
انواع داده
CTS دادهها را به دو نوع تقسیم میکند:
نوع مقداری (Value Type)
نوع مرجعی (Refrence Type)
انواع دادهای توده سادهای از داده میباشند. نمونههای انواع دادهای نه هویت مرجعی دارند و نه مفاهیم مقایسه مراجع را. برای مقایسه برابری یا عدم برابری انواع دادهای، خود مقدار دادهها را با یکدیگر مقایسه میکنیم مگر اینکه عملگرهای مشابه دوباره تعریف شده باشند. مقادیر دادههای مرجعی همیشه یک مقدار پیشفرض دارند و همیشه میتوانند ایجاد یا کپی شوند. یکی دیگر از محدودیتهای انواع دادهای این ات که آنها نمیتوانند از یکدیگر مشتق شوند (ولی میتوانند اشتراکاتی داشته باشند) و هم چنین نمیتوانند در سازنده مقدار دهی اولیه شوند. مثالی از انواع دادهای، بعضی از انواع اولیه مانند int و float و char و System.DateTime میباشند. در مقابل، انواع مرجعی مفهوم تعریف مرجعی را دارند (که در آن هر نمونه از نوع مرجع، بهطور ذاتی از دیگر نمونهها جدا میشود، حتی اگر داده هر دو نمونه یکی باشد). این دقیقاً نمونه مشابه مقایسه تساوی یا عدم تساوی دادههای مرجعی است، که در آن آزمایش برای مرجعها از دادهایها سریع تر است. در کل نه همیشه امکان تعریف نمونه مرجعی وجود دارد و نه امکان کپی یا نمایش مقادیر مقایسه دو نمونه؛ ولی به هر حال انواع مرجعی خاص میتوانند این اعمال را از طریق سازندههای عمومی یا اجرای واسطهای مشابه (مثل ICloneable یا IComparable) انجام دهند. نمونههایی از انواع مرجعی، اشیاء، System.String و Sysmet.Array میباشند. هر دو نوع داده قابلیت انعطاف توسط تعریف به وسیله کاربر را دارند. در واقع وقتی ما نوع دادهای را به تابع ای ارسال میکنیم، آدرس داده نیز فرستاده میشود. البته این امر پیشفرض است ولی برای دادههای مثل آرایه، رشتهای، آدرس فرستاده میشود و ارسال از نوع مرجع میشود
برنامهنویسی شیگرا (به انگلیسی Object-Oriented Programming مخفف:OOP) یک شیوه برنامهنویسی است که ساختار یا بلوک اصلی اجزای آن، شیها میباشند. در واقع در این شیوه برنامهنویسی، برنامه به شی گرایش پیدا میکند. به این معنا که دادهها و توابعی که قرار است بر روی این دادهها عمل کنند، تا حد امکان در قالبی به نام شی در کنار یکدیگر قرار گرفته، جمعبندی شده و یک واحد (شی) را تشکیل داده و نسبت به محیط بیرونِ خود، کپسوله میشوند و از این طریق، توابع بیگانهٔ خارج از آن شی، دیگر امکان ایجاد تغییر در دادههای درون آن شی را ندارند. بهطور مثال حساب بانکی شما که شامل مشخصات فردی شما و میزان سپردهٔ شما در بانک است، تشکیل یک شی را میدهند و به دلیل دارا بودن ویژگی کپسوله، امکان دستکاری در میزان سپرده یا مشخصات شما، توسط دیگران وجود ندارد از دیگر ویژگیهای برنامهنویسی شی گرا، پیچیدگی کم، هزینه کم، امکان گسترش سریع برنامه با خطای کمتر نسبت به سایر پارادایمهای برنامهنویسی است.
رشته ها
در C یا ++C ساختار رشته به صورت ارایهای از نوع char بود که امکان اضافه کردن به رشته را محدود میکرد به دلیل ثابت بودن طول در آغاز تعریف ولی در سی شارپ دو نوع متفاوت رشته وجود دارد؛ که یکی به صورت آرایهای با طول ثابت ۲۵۶(در عمل ۲۵۵)موجوداست (به صورت پیش فرض) و در صورتی که با کمبود جا روبرو شود فضای جدید (بزرگتر) یافته و به ان انتقال میدهد؛ ولی در نوع دوم رشتهها از لیست پیوندی استفاده میشود.
***لیست پیوندی***
یست پیوندی (به انگلیسی: Linked list) ساختاری شامل دنبالهای از عناصر است که هر عنصر دارای اشارهگری به عنصر بعدی در دنباله است. فهرست پیوندی از جملهٔ سادهترین و رایجترین دادهساختارها است و در پیادهسازی از دادهساختارها پشته (Stack)، صف (Queue) و جدول درهمسازی (Hash table) استفاده میشود. مزیت مهم فهرست پیوندی نسبت به آرایهها این است که ترتیب قرار گرفتن دادهها در آن با ترتیب قرار گرفتن آنها در حافظه متفاوت است. به همین دلیل فهرست پیوندی دارای این ویژگی است که درج و حذف گرهها در هر نقطهای از فهرست، با تعداد ثابتی از عملیات امکانپذیر است. از طرف دیگر فهرست پیوندی اجازه دستیابی تصادفی به داده یا هرگونه اندیسگذاری را نمیدهد. در نتیجه بسیاری از اعمال ابتدایی نظیر به دست آوردن آخرین عنصر فهرست، پیدا کردن عنصر شامل داده مورد نظر، یا مشخص کردن مکان درج یک عنصر جدید ممکن است نیازمند بررسی اکثر عناصر فهرست باشد.